How to Cron: Advanced Data Structures for Discrete Event Simulation
On algorithmic improvements in the event set management, from O(√n) to O(1).
Recently, I was working on a service whose main responsibility was to schedule tasks and trigger their run at regular intervals. As with all projects, I check to see what's out there and if there are solutions that have been proved better and more efficient than what I already had in mind. So, I started looking into how the unix cron is doing its scheduling and stumbled upon a couple of interesting data structures that I wanted to take a deep dive into. Here's what I hope is a successful summary.
The early cron days
The original cron was designed by Ken Thompson in Unix V7 (around 1979) and was later rewritten by Dennis Ritchie. It used to work in a simple way. It would read the crontab files from /usr/lib/crontab, used a simple in memory table for job scheduling and had one main process that woke up every minute and determine if any commands must run at the current date and time, and if so, run them as the superuser, root.
This method presented a couple of challenges. It could easily overload the system if too many jobs ran simultaneously. It consumed resources every minute whether there was a job to be run or not. Performance degraded with more entries. It wasn’t suitable for large systems with many users. Memory usage grew linearly with number of jobs. There was no way to limit the number of jobs per user.
These limitations led to the development of more sophisticated cron implementations for multi-user capability.
The Franta-Maly Event List Approach
The Unix System V came with an upgraded version of cron based on the 1977 paper by W.R. Franta and Kurt Maly, An Efficient Data Structure for the Simulation Event Set. [1] In this paper, they presented a new event scheduling algorithm that improves on previously published algorithms. Robert Brown, a Purdue graduate student, noticed similarities between cron and discrete event simulators, leading him to implement the Franta-Maly event list manager. In 1979, Keith Williamson, a new graduate student, developed Brown's prototype into a production-ready multi-user cron service at Purdue.
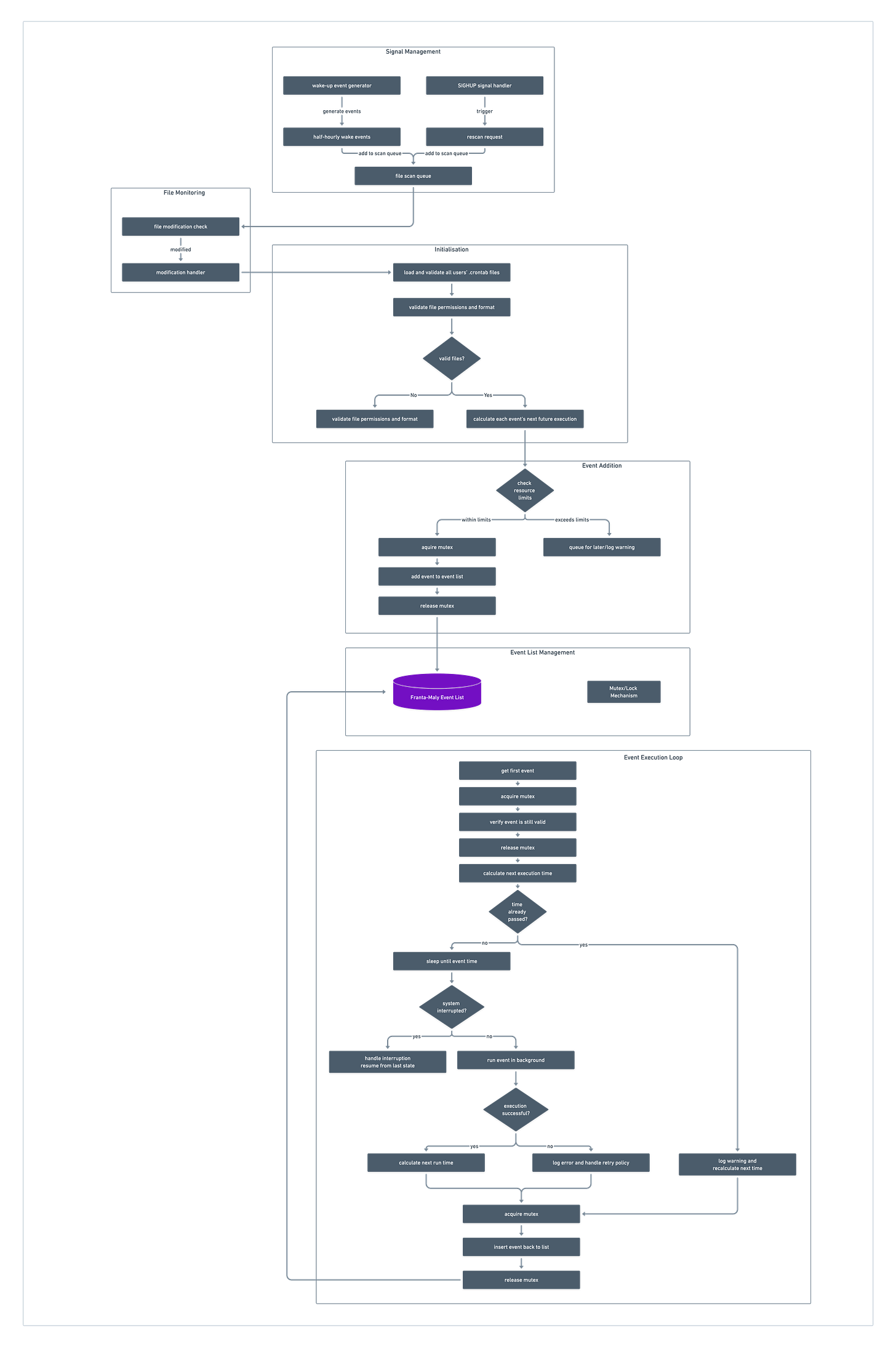
The cron algorithm begins by searching for .crontab files in all users' home directories at startup. For each discovered crontab file, it calculates the next future execution time for each command and adds these commands to the Franta-Maly event list, along with their execution times and five-field time specifiers. The main loop then continuously examines the first task in the queue, calculating its future execution time. The system sleeps until that time, then wakes to verify the time and execute the queued task in the background using the original user's privileges. After execution, it recalculates the next runtime for that command and reinserts it into the event list accordingly.
The daemon implements two monitoring mechanisms for crontab file changes: it processes SIGHUP signals to trigger immediate rescans of modified crontab files, and it maintains scheduled wake-up checks at 30-minute intervals (on the hour and half-hour) to detect any crontab modifications.
The Franta-Maly event list (Two-Level algorithm) has a time complexity of O(√n) in the worst case scenario, driven by its two-tier data structure design and event insertion mechanism.
The Two-Level (TL) Algorithm Data Structure
The Two-Level (TL) algorithm proposed by Franta and Maly utilises a sophisticated data structure to efficiently manage event notices in discrete event simulations. The primary goal of this structure is to reduce the number of comparisons required to find the correct position to insert a new event notice, thus optimising the simulation's performance. The algorithm utilises a data structure inspired by indexed lists and balanced tree concepts (3-2 trees), to minimise the computational cost of scheduling and processing events.
The data structure consists of 3 layers:
the index list layer - The TL algorithm uses an index list to divide the range of event times into a number of equal-sized intervals. Each element in the index list points to a "dummy key" which represents the boundary of an interval.
the secondary key layer - The efficiency of the TL algorithm lies in the introduction of secondary keys within each interval. These keys, associated with the right boundary dummy key, point to sublists of event notices within the interval. This two-level indexing scheme enables more efficient searching and insertion operations.
the event notices layer - Each interval is further divided into sublists, each headed by a secondary key. The sublists are designed to be balanced, meaning they don't grow excessively large. The maximum size of each sublist is controlled by nlim parameter.
The Insert Operation - Worst Case Complexity: O(√n)
Let’s say we want to insert a new event with t=1.3. The Franta-Maly insertion process follows a systematic sequence through the data structure's layers. First, we calculate the target interval by applying the formula i = [(t - lowerbound)/dt] to determine the precise interval containing the event time, which leads us to the corresponding dummy key entry in the index list.
Next, we traverse the sequence of secondary keys associated with the identified dummy key until locating the appropriate insertion point. For an event with time t=1.3, this involves scanning until we find it belongs between secondary keys 1.2 and 1.5.
The actual insertion occurs by placing the event notice in its correct time-ordered position within the identified sublist. In our example, the new event with t=1.3 is inserted between existing events with times 1.2 and 1.4, maintaining the temporal ordering of the sublist.
Finally, we execute a balance check to maintain the data structure's efficiency. The system verifies if the insertion has caused the sublist to exceed its maximum size (nlim). When the size limit is exceeded, the structure triggers one of two rebalancing operations: either transferring the last notice to an adjacent list or creating a new secondary key. If the sublist remains within size constraints, the insertion completes without requiring rebalancing.
The worst case complexity occurs when all n notices are associated with the same dummy key and the new event being inserted has a time smaller than all other notices in the structure. The complexity is calculated as: cw(n) = n/nlim + nlim, where nlim is optimally set to √n to minimize the worst case complexity.
The Search Operation - Worst Case Complexity: O(√n)
Let’s say we want to search for an event with t=1.3.
The search process in the Franta-Maly structure executes in three sequential phases. The first phase calculates the target interval using the formula i = [(t - lowerbound)/dt], which maps directly to the corresponding dummy key in the index list. This initial lookup operates in constant time O(1).
The second phase traverses the secondary key sequence within the identified interval until locating the appropriate sublist. For a target time t=1.3, the algorithm scans between secondary keys 1.2 and 1.5, ultimately selecting SK2's sublist. This traversal has a worst-case complexity of O(√n).
The final phase executes a linear search within the selected sublist to find the exact match or appropriate position. Since the maximum sublist size is constrained by nlim (√n), this search also operates with worst-case complexity O(√n). The combination of these three phases yields an overall worst-case complexity of O(√n), though practical performance often approaches constant time.
Calendar Queues (CQ)
A calendar queue is a priority queue data structure specifically designed for efficient handling of time-based events. It was introduced by Randy Brown in 1988 [2] and is particularly useful in discrete event simulation systems.
The queue is organized like a calendar, divided into "buckets" (like days or time slots). Each bucket represents a fixed-width time interval. Events within each bucket are sorted by their timestamp. The buckets are arranged in a circular array (wrapping around like a year calendar)
The data structure consists of 4 components:
Buckets: An array representing days in a year, each element pointing to a sorted linked list of events scheduled for that day.
Event Nodes: Contain information about the event, including its time (priority) and any associated data. These are organised into sorted linked lists within each bucket.
Circular Calendar: Events can be scheduled up to a year in advance. Once the last day of the year is reached, the calendar wraps around to the first day, allowing for continuous event scheduling without data structure manipulation2.
Event Dates: Each event node stores its scheduled date to handle events scheduled beyond a year. Events with future dates are skipped during dequeue operations until the calendar reaches their scheduled year
The above image shows how Brown’s Calendar Queue looks like, where the year starts at 12.0 and end at 16.0 and the bucket width is 0.5 time units.
How are events inserted?
Events are assigned to buckets using this formula:
bucket_number = floor(priority/bucket_width) % number_of_bucketsLet’s say we want to insert a new element 14.6 and we have the following initial state:
We have the current year that starts at 12.0 and ends at 16.0 (range of 4.0 units), with a bucket width = 0.5 time units and 8 buckets. We calculate the
bucket_number = floor(14.6/0.5)%8 = 29%8 = 5The element belongs to bucket 5 and will be inserted into sorted position into the bucket’s linked list.
This insertion process maintains O(1) average complexity since bucket calculation is O(1), each bucket contains a small, roughly constant number of events, and searching within a bucket's linked list is therefore bounded by a constant.
How is bucket width calculated?
According to Brown's paper, the bucket width is calculated in a clever way to maintain efficiency:
bucket width is adjusted each time the queue is copied onto a new calendar (when resizing)
events are sampled to find the average separation:
For small queues (≤ 5 events): sample all events
For larger queues: sample 5 + size/10 events (up to max of 25 samples)
Dequeue these events, record their priorities, then re-insert them
there’s a two-step average calculation:
First calculate initial average separation between sampled events
Then recalculate average using only separations smaller than twice the initial average (this handles bimodal distributions by ignoring large gaps)
and finally, the bucket width = 3.0 * final average
The reasoning behind this method is that we aim to have 2-3 events per bucket on average. Multiplier of 3.0 was found experimentally to give best performance. Ignoring large gaps helps handle skewed/bimodal distributions. Using a sample rather than all events makes the calculation efficient.
When does resizing occur?
According to Brown's paper, resizing occurs based on queue size thresholds, more specifically:
Growing (Doubling):
Resize occurs when queue size > 2 * number_of_buckets
The new calendar gets twice as many buckets
Example: If current size is 50 buckets, resize at 101 events
Shrinking (Halving):
Resize occurs when queue size < number_of_buckets/2
The new calendar gets half as many buckets
Example: If current size is 50 buckets, resize at 24 events
During the resizing process, a new calendar array is created, a new bucket width is calculated using the sampling method, all events are copied to their new bucket positions and finally the switch to the new calendar is done.
Brown analyzed the impact of resizing, the average event is copied less than 2 times during its lifetime. In the worst case, the queue size oscillates between just above 2^n and just below 2^(n-1), and even in worst case, only about 3 events are copied per hold operation.
The key innovation of Brown's Calendar Queue was simplifying the two-level approach by using fixed-size buckets instead of dynamic sublists, eliminating the overflow problem through circular wrapping and providing automatic adaptation through bucket resizing. This made the Calendar Queue both simpler to implement and more efficient in practice compared to the TL algorithm, especially for larger queue sizes and varying event distributions.
FELT - An optimisation to CQ
One of the disadvantages of Brown’s CQs is that resize operation would involve creating a new CQ structure and then moving each item from the old CQ to the new CQ before discarding the old CQ. Hence, such resizes can be costly if the size of the queue is very large. And this is what Hui’s and Thng’s FELT (Far Future Event Leaf Tree) [3] structure is trying to solve.
FELT uses two different structures together to manage events:
A regular calendar queue for near-future events (Primary Tier)
A special tree structure for far-future events (FELT) (Secondary Tier)
Primary Tier (Calendar Queue)
Works like a normal calendar queue with a fixed maximum size (typically 4096 events)
The FELT primary Calendar Queue works like a normal calendar queue with dual thresholds. The UPPBOUND threshold, typically set at 4096 events, represents the maximum capacity of the primary queue. When exceeded, the system initiates a transfer operation, moving the oldest events into the secondary tree structure. This transfer specifically moves UPPBOUND minus LOWBOUND events, maintaining optimal queue size for performance.
Conversely, the LOWBOUND threshold, typically set at 256 events, establishes the minimum required event count in the primary queue. When the queue size drops below LOWBOUND, the system initiates a replenishment operation. During replenishment, the system identifies the leaf node containing events with the earliest timestamps in the secondary tier, transfers its entire contents to the primary queue, and removes the depleted leaf node. This process ensures the primary queue maintains sufficient events for efficient operation.
Secondary Tier (Tree Structure)
FELT acts as a semi sorted binary tree, where the left branch always holds events with higher priority (earlier timestamps) than the right branch. Only the leaf nodes store events. These events are kept in an unsorted linked list called NodeList. Parent nodes act as branching points. They do not store events themselves but maintain information about the minimum timestamp (MinTimeStamp) of all events in the branches below them. This helps efficiently route new events to the correct leaf node during insertion.
FELT is size-based, meaning it manages events based on the number of events stored in the primary CQ. This contrasts with time-based approaches like the Future Event Tree (FET) used in the Dynamic Lazy Calendar Queue (DLCQ), which can lead to inefficiencies when the CQ resizes.
[Parent Node(PN): MinTimeStamp(t) = X]
/ \
[Parent Node: MinTimeStamp = Y] [Parent Node: MinTimeStamp = Z]
/ \ / \
[Leaf Node(LN): MinTimeStamp = A] ... ... [Leaf Node: MinTimeStamp = B]
| |
[Unsorted Linked List of Events(ULLE)] [(ULLE)]How are events inserted?
FELT processes each new event through a two-stage decision process for optimal placement. Initially, the system examines the event's timestamp to determine whether it belongs in the near-future or far-future category. This classification happens by comparing the event's timestamp against a threshold calculated as the current simulation time plus one calendar period.
For near-future events, the system directs them into the primary calendar queue using standard calendar queue insertion operations. However, if this insertion causes the primary queue to exceed its size threshold, the system automatically transfers the oldest events from the primary queue into the secondary tree structure to maintain optimal queue performance.
Far-future events take a different path, entering the secondary tree structure where they navigate through internal nodes based on timestamp comparisons. The event travels down the tree, with each internal node guiding it left or right until it reaches an appropriate leaf node. Once at the leaf node, the event is simply appended to an unsorted list maintained at that node:
Start at the Top Node: The insertion process begins at the topmost node of the FELT structure (TopNode).
Check if Current Node is a Leaf Node:
If the current node is a leaf node: The event is inserted into the unsorted linked list (NodeList) at that leaf node.
If the current node is a parent node: Proceed to step 3.
Compare Event Timestamp with Right Child's MinTimeStamp:
If the event's timestamp is greater than or equal to the MinTimeStamp of the right child node, AND the right child node is not NULL: Move to the right child node and repeat step 2.
Otherwise: Proceed to step 4.
Check Left Child:
If the left child node is not NULL: Move to the left child node and repeat step 2.
Otherwise: Insert the event into the NodeList of the current node (which must be a leaf node).
Check for Node Splitting: After the event is inserted, the algorithm checks if the leaf node has exceeded its maximum capacity (MaxSize). When a leaf node has reached its maximum capacity (MaxSize) of events that it can store, which is set a priori, it will spawn two new leaf nodes and split NodeList into 2 and transfer the events into the left and right leaf nodes.
If the node needs splitting: The splitNode function is called to create two new child leaf nodes and redistribute the events based on their timestamps.
[Parent Node(PN): MinTimeStamp(t) = 10]
/ \
[PN:t = 5] [PN:t = 15]
/ \ / \
[LN:t = 2] [LN:t = 7] [LN:t = 12] [LN:t = 17]
| | | |
[(ULLE)] [(ULLE)] [(ULLE)] [(ULLE)]New Event (Timestamp = 8)
Start at TopNode (MinTimeStamp = 10).
8 < 15 (Right Child's MinTimeStamp), so move to Right Child (MinTimeStamp = 12).
Left Child is NULL, so insert event into current node.
Result:
[Parent Node(PN): MinTimeStamp(t) = 8]
/ \
[PN:t = 5] [PN:t = 8]
/ \ / \
[LN:t = 2] [LN:t = 7] [LN:t = 8] [LN:t = 17]
| | | |
[(ULLE)] [(ULLE)] [(ULLE)] [(ULLE)]
|
[New Event (Timestamp = 8)]When it comes to complexity, the tree traversal is O(log n) in best case when tree is balanced and O(n) when it’s a completely skewed tree.
While the theoretical worst case is O(n), the actual performance in practice tends toward O(1) because: the size-based splitting keeps the tree reasonably balanced. The large maxSize (3840) means splits are rare, no sorting is required within leaf nodes and the split cost is bounded by a constant.
The authors show empirically that FELT maintains near O(1) performance even for large queue sizes and skewed event distributions, performing better than other approaches like DLCQ.
The Snoopy CQ
The Snoopy Calendar Queue, proposed by Tan, Kah Leong, and Li-Jin Thng. "SNOOPy Calendar Queue." [4], builds upon the concepts of the conventional Calendar Queue (CQ) and the Dynamic Calendar Queue (DCQ), addressing their limitations, particularly in handling skewed event distributions. SNOOPy CQ extends the calendar queue with statistical optimization mechanisms. Instead of using sampling for bucket width calculation like traditional CQ, it tracks operational costs and uses these statistics to optimize queue parameters. The name "SNOOPy" stands for Statistically eNhanced with Optimum Operating Parameter Calendar Queue. The core of SNOOPy CQ lies in its ability to dynamically adjust its operating parameter – the bucket width – based on the queue's performance statistics. This adaptive mechanism ensures consistent and efficient performance, achieving near-O(1) complexity even in challenging scenarios.
+-----------------------+
| SNOOPy CQ |
+-----------------------+
| ^
| |
v |
+-----------------------+
| Enqueue/Dequeue |
| Operations |
+-----------------------+
| ^
| |
v |
+-----------------------+
| Performance Statistics|
| (CE, CD) |
+-----------------------+
| ^
| |
v |
+---------------+-----------------------+----------------+
| | | |
v v v v
+-------------+-------------------+--------------+--------------+
|Trigger Check| Bucket Width |Calendar Resize| Cost |
| (CE, CD, | Optimization | (BW, NB) | Calculation |
| Thresholds) |(Minimize CE + CD) | | (CE, CD) |
+-------------+-------------------+---------------+--------------+Enqueue/Dequeue Operations: These are the fundamental operations performed on the SNOOPy CQ. Events are enqueued (added to the queue) based on their timestamps, and the event with the earliest timestamp is dequeued (removed from the queue) for processing.
Performance Statistics Collection: As events are enqueued and dequeued, SNOOPy CQ meticulously tracks two crucial performance metrics:
Average Enqueue Cost (CE): This represents the average number of events traversed before an insertion can be made in a bucket's linked list.
Average Dequeue Cost (CD): This signifies the average number of buckets that need to be examined before finding the event with the earliest timestamp.
Trigger Check: SNOOPy CQ continuously monitors the collected performance statistics (CE and CD). It employs multiple trigger mechanisms:
Inherited from CQ and DCQ: These triggers are based on thresholds for CE and CD (e.g., if either exceeds a value of 2 or 3), as in the CQ and DCQ structures.
Unique to SNOOPy CQ: Additional triggers are based on the relative difference between CE and CD over multiple slots (time intervals corresponding to a certain number of enqueue or dequeue operations). If the difference exceeds a predefined factor, it signals a need for adjustment.
Bucket Width Optimization: When any of the trigger conditions are met, indicating a suboptimal bucket width, SNOOPy CQ initiates its bucket width optimization process. The goal is to find a new bucket width (BW) that minimizes the total cost (CE + CD), keeping the number of buckets (NB) constant. SNOOPy CQ employs a novel approach to determine the optimum BW based on the relationship between CE and CD, as detailed in section 3.1 of "download.pdf".
Calendar Resize: Once the optimal bucket width is calculated, the SNOOPy CQ undergoes a resize operation. A new calendar queue is created with the calculated BW and the same NB as before. Events from the old calendar are then transferred to their appropriate buckets in the new calendar.
Cost Calculation: After each slot (a series of enqueue or dequeue operations), the average enqueue cost (CE) and average dequeue cost (CD) are recalculated based on the accumulated statistics from that slot. These updated costs are then used in subsequent trigger checks and optimization processes.
Conclusion
Starting from the simple Unix V7 cron implementation, each subsequent event scheduling structure addressed specific limitations of its predecessors.
The Franta-Maly event list introduced sophisticated two-level indexing, achieving O(√n) complexity through its hierarchical structure. Brown's Calendar Queue (CQ) then simplified this approach with fixed-size buckets and circular wrapping, providing O(1) average performance for uniform distributions.
FELT built upon CQ's foundation by introducing a dual-tier architecture that efficiently manages near and far-future events, effectively addressing the resize overhead issues. Its size-based approach, rather than time-based, provides consistent performance across varying event distributions.
SNOOPy CQ represents the current state-of-the-art, employing statistical optimisation to dynamically adjust bucket widths based on operational costs. This adaptive approach ensures robust O(1) performance even under skewed distributions.
Data Structures Comparison
Franta-Maly Structure (1977)
Primary Components
Employs a two-level structure based on indexed lists and the balanced terminal node structure of 3-2 trees.
Divides the range of event times into intervals, bounded by "dummy keys (notices)" pointed to by an index list.
Each interval further divided into sublists, marked by secondary keys associated with the right boundary dummy key.
Key Operations Performance
Insertion (O(√n) worst case):
Binary search index array to find appropriate terminal node
Linear search within terminal node for insertion position
Split terminal node if size exceeds 2√n
Update index pointers if split occurs
Deletion (O(√n) worst case):
Search index array for target terminal node
Remove event from terminal node
Merge underfull terminal nodes if necessary
Update index pointers after merge
Terminal Node Management:
Split Threshold: 2√n events
Merge Threshold: ½√n events
Maintains roughly balanced terminal node sizes
Performance Bottlenecks
Index Array Search:
Binary search cost increases with structure size
More frequent searches in skewed distributions
Terminal Node Operations:
Linear search within nodes
Split/merge overhead with uneven distributions
Maintenance Overhead:
Index updates after node modifications
Balance maintenance across terminal nodes
Advantages, Limitations and Selection Criteria
Advantages:
Bounded Operations:
Guaranteed O(√n) worst case
Predictable performance characteristics
Memory Locality:
Events clustered in terminal nodes
Efficient cache utilisation for sequential access
Flexible Structure:
Adapts to varying event distributions
Self-balancing capabilities
Consider Using When:
Predictable Performance is critical:
Operations must have guaranteed bounds
Worst-case performance matters more than average case
Memory Access Patterns are important:
System benefits from clustered event storage
Cache efficiency is a priority
Limitations:
Complex Implementation:
Significant code complexity for node management
Error-prone split/merge operations
Performance Issues:
High overhead for small event sets
Degraded performance with skewed distributions
Maintenance Overhead:
Frequent index updates
Complex rebalancing operations
Avoid Using When:
Simple Implementation is preferred:
Calendar queue or modern alternatives offer simpler solutions
Development time is constrained
Optimal Average Performance is required:
Calendar queue provides better average-case performance
Event distribution is relatively uniform
Calendar Queue (Brown, 1988)
Primary Components
Based on the analogy of a desk calendar, with each "day" represented by a sorted linked list. An array of pointers provides access to each day's linked list.
Bucket Array:
Fixed-size array of bucket heads
Each bucket contains sorted linked list of events
Array size maintained as power of 2 for efficient modulo operations
Circular structure with wrap-around for year boundaries
Year Mechanism:
Year = NB * BW (Number of buckets * Bucket width)
Tracks current year for wrap-around handling
Enables infinite future time handling with finite structure
Key Operations Performance
Enqueue (O(n) worst case, O(1) average case):
Calculate virtual bucket using timestamp
Map to actual bucket using modulo
Insert in sorted order within bucket
O(n) complexity when all events are in one bucket
Dequeue (O(n) worst case, O(1) average case):
Start from lastBucket
Remove earliest event from current bucket
Advance to next bucket if empty
Handle year wrap-around when needed
O(n) when searching empty buckets
Resize (O(n)):
Triggered when queue size crosses thresholds:
Upsize: size > 2 * nbuckets
Downsize: size < nbuckets/2
Creates new bucket array with doubled/halved size
Recalculates bucket width by sampling
Redistributes all events
Performance Bottlenecks
Bucket Width Impact:
Too small: Events spread across too many buckets
Too large: Too many events per bucket
Optimal: 2-3 events per bucket near dequeue point
Distribution Effects:
Uniform: Achieves O(1) performance
Skewed: Performance degrades
Bimodal: May require frequent resizing
Advantages, Limitations and Selection Criteria
Advantages:
Uniform Distributions - for network simulation, regular event patterns, predictable timings etc
Medium-sized Queues - for 1,000 to 10,000 events, stable event counts, regular dequeue patterns
Limitations:
Skewed Distributions - lead to performance degradation, frequent resizing, bucket imbalance
Very Large Queues - lead to resize overhead, memory locality issues, width calculation challenges
FELT (Far Future Event Leaf Tree, 2002)
Primary Components
Uses a Primary Tier (Calendar Queue) and a Secondary Tier (Tree Structure).
Primary Tier (Calendar Queue):
Works like a normal calendar queue with a fixed maximum size (typically 4096 events)
Has both an upper limit (UPPBOUND) and lower limit (LOWBOUND) for number of events
When too full, moves events to the secondary tier
When too empty, gets events back from the secondary tier
Secondary Tier (Tree Structure):
Uses a binary tree where only leaf nodes store events
Leaf nodes contain unsorted lists of events
Parent nodes just help route to the right leaf node
Each node keeps track of the smallest timestamp in its subtree
Key Operations Performance
When Adding a New Event:
Decision Point: System first checks if the event is near-future or far-future
Near-Future Events:
Go directly into the calendar queue
If this makes the queue too full, oldest events are moved to the tree
Far-Future Events:
Go into the tree structure
Get routed down the tree to the appropriate leaf node
Added to that leaf node's unsorted list
Near-future events (Primary Calendar Queue): O(1) average case, as it uses standard calendar queue insertion
Far-future events (Secondary Tree): O(log n) to traverse the tree to the correct leaf node, then O(1) to append to unsorted list
Overall: O(1) for near events, O(log n) for far events
When Retrieving Events:
Always take events from the calendar queue first
When calendar queue gets too empty:
Find the leaf node with earliest events in the tree
Move those events to the calendar queue
Continue processing from calendar queue
Primary Calendar Queue: O(1) average case
When primary queue needs replenishment:
Finding minimum leaf node: O(1) using tree's cached minimum timestamps
Transferring batch of events: O(k) where k is transfer batch size
Overall: Amortized O(1) since transfer costs are spread across many operations
Performance Bottlenecks
Transfer Operations Impact:
When the primary queue hits its UPPBOUND or LOWBOUND thresholds, the transfer operations between tiers can cause significant overhead. These transfers require moving large batches of events between structures and can temporarily pause normal operations. While the cost is amortized, it can cause noticeable performance spikes.
Leaf Node Management:
When leaf nodes in the secondary tier get too full and need splitting, the operation requires scanning all events in the node to find the average timestamp, then redistributing them. This can be expensive for large leaf nodes and may happen frequently with certain event patterns.
Threshold Tuning:
Choosing optimal values for UPPBOUND and LOWBOUND is critical but challenging. Poor choices can lead to either too frequent transfers or inefficient primary queue operation, significantly impacting performance.
These bottlenecks become particularly apparent in scenarios with:
- Highly skewed temporal distributions
- Memory-constrained environments
- Large numbers of far-future events
Advantages, Limitations and Selection Criteria
Optimal Use Cases
Large Event Sets (10,000 events)
Wide timestamp distribution
Frequent far-future events
Variable Distributions:
Skewed timestamp patterns
Mixed temporal localities
Dynamic workload patterns
Limitations
Implementation Complexity:
Complex maintenance logic
Debugging challenges
Higher development overhead
Resource Requirements:
Additional memory overhead
Complex pointer management
Transfer operation costs
SNOOPy Calendar Queue (2000)
Primary Components
The structure maintains traditional calendar queue elements plus statistical tracking:
Calendar Base Structure:
Array of buckets containing sorted event lists
Each bucket represents a time interval
Year size = number of buckets × bucket width
Statistical Enhancement Layer:
CE (Enqueue Cost): Tracks average number of events traversed during insertion
CD (Dequeue Cost): Tracks average number of empty buckets traversed during dequeuing
Moving average window over multiple operations
Performance metrics for bucket width optimisation
Key Operations Performance
Enqueue Process (O(1) average case):
Calculates target bucket using timestamp
Inserts event in sorted order within bucket
Updates enqueue cost statistics based on traversal length
Triggers resize if statistical thresholds exceeded
Dequeue Process (O(1) average case):
Retrieves earliest event from current bucket
Advances through empty buckets if necessary
Updates dequeue cost statistics
May trigger optimisation based on performance metrics
Resize Operation (O(n) when restructuring):
Triggered by statistical cost metrics rather than just size
Uses performance history to calculate optimal bucket width
Redistributes events across new structure
Resets statistical counters after resize
Performance Bottlenecks
Statistical Overhead:
Continuous cost tracking adds per-operation overhead
Moving average calculations require additional computation
Statistical threshold checks on every operation
Resize Decisions:
More complex than traditional CQ resize triggers
May require more frequent resizes initially while optimising
Statistical calculation overhead during resize operations
Dynamic Adaptation:
Initial period of suboptimal performance while gathering statistics
May oscillate between different configurations before settling
Additional memory references for statistical tracking
Advantages, Limitations and Selection Criteria
Advantages:
Robust Performance:
Better handling of skewed distributions than traditional CQ
Self-tuning capability reduces manual parameter tuning
More consistent performance across varying workloads
Adaptive Optimisation:
Automatically adjusts to changing event patterns
Reduces impact of poor initial parameter choices
Maintains efficiency under varying conditions
Statistical Insight:
Provides performance metrics for monitoring
Enables informed optimization decisions
Can predict and prevent performance degradation
Best Used When:
Event distribution is unknown or varies
Long-running simulations justify optimization overhead
Performance consistency is critical
Manual tuning is impractical
Limitations:
Implementation Complexity:
More complex than basic calendar queue
Additional overhead for statistical tracking
More difficult to debug and maintain
Avoid When:
Simple, known event distributions
Short-running simulations
Memory or CPU resources are very constrained
Implementation simplicity is priority
Resources
[1] Franta, W. R., and Kurt Maly. "An Efficient Data Structure for the Simulation Event Set." Communications of the ACM 20, no. 8 (August 1977): 596-602.
[2] Brown, Randy. "Calendar Queues: A Fast O(1) Priority Queue Implementation for the Simulation Event Set Problem." Communications of the ACM 31, no. 10 (October 1988): 1220-1227.
[3] Hui, Timothy Chee-Kin, and Ian Li-Jin Thng. "FELT: A Far Future Event List Structure Optimized for Calendar Queues." SIMULATION: Transactions of The Society for Modeling and Simulation International 78, no. 6 (June 2002): 343-361.
[4] Tan, Kah Leong, and Li-Jin Thng. "SNOOPy Calendar Queue." In Proceedings of the 2000 Winter Simulation Conference, edited by J. A. Joines, R. R. Barton, K. Kang, and P. A. Fishwick, 487-495. IEEE, 2000.