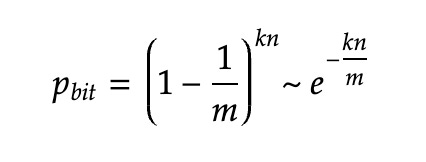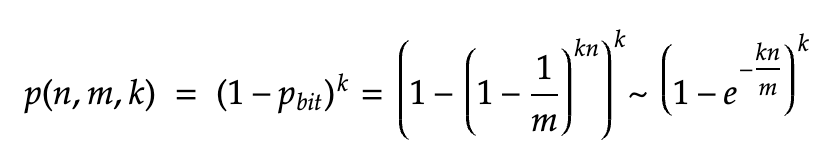Optimising Performance: The Cool Magic of Bloom Filters
This is the first part of a System Design Patterns series where we dive into a system design problem and present possible ways to approach it.

Motivation
When you have a large set of structured data (identified by record IDs) stored in a set of data files, what is the most efficient way to know which file might contain our required data? We need to keep track of large entities with the smallest memory print possible.
Reading each file would be slow as we have to read a lot of data from the disk. We could build an index on each data file and store it in a separate index file. Each index file will be sorted on the record ID. If we want to search an ID in this index, the best we can do is a Binary Search. Would there be an even faster approach?
Solution
A Bloom filter is a probabilistic data structure, named after Burton Howard Bloom, who invented them in the 1970s. It is based on hashing designed to tell you, rapidly and memory-efficiently, whether an element is present in a set. Elements are not added to the set but their hash is.
The price paid for this efficiency is that a Bloom filter is a probabilistic data structure: it tells us whether the element is either definitely not in the set or that it may be in the set, thus false positives are possible.
How does it work?
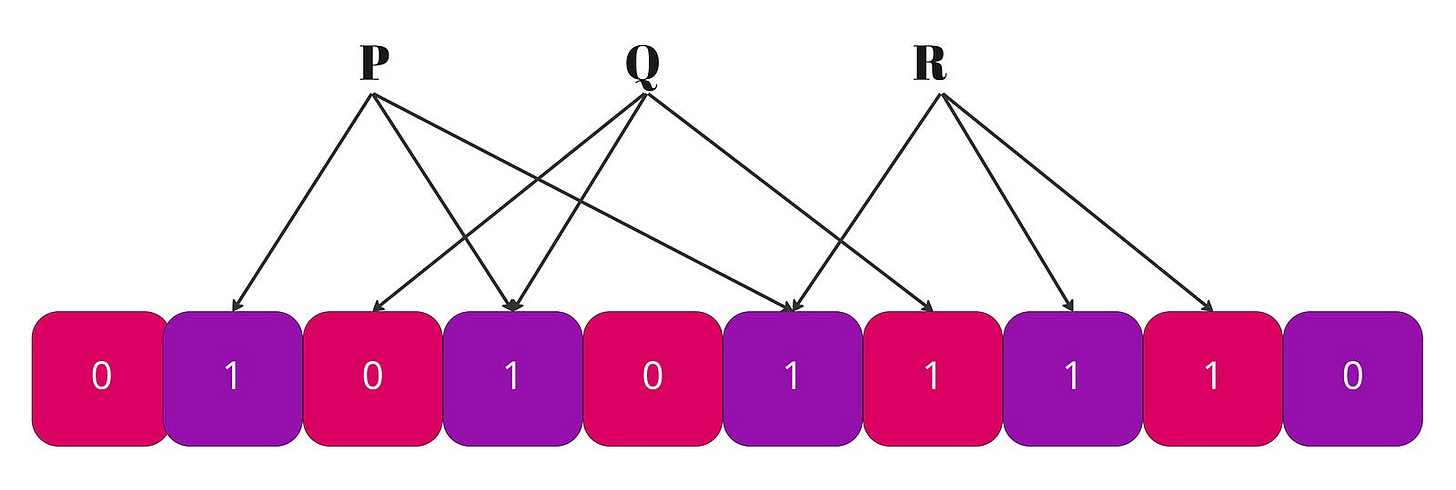
A Bloom filter is made of two elements: an array of
melements and a set ofkhash functions. An empty Bloom filter is a bit-array ofmbits, all set to 0 initially; and each hash function outputs an index between0andm-1. There is no1-1correspondence between the elements of the array and the keys we add to the Bloom filter. We usekbits to store each entry for the Bloom filter.kis a constant that we pick when we create the data structure, so each and every entry we add is stored using the same amount of memory,kbits.To add an element, feed it to the hash functions to get
kbit positions, and set the bits at these positions to 1.To test if an element is in the set, feed it to the hash functions to get
kbit positions:
1. If any of the bits at these positions is 0, the element is definitely not in the set.
2. If all are 1, then the element may be in the set.
Choosing the Hash Functions
The hash functions used in a Bloom filter should be independent and uniformly distributed. Some examples of independent enough include murmur, xxHash, the fnv series of hashes, and HashMix. The more hash functions you have, the slower your bloom filter, and the quicker it fills up. If you have too few, however, you may suffer too many false positives.
The false-positive ratio formula
The false positive rate of your filter can vary on the length of the filter. A larger filter will have less false positives, and a smaller one more. Considering that
n = number of elements you expect to insert,
m = number of bits in the bloom filter and
k = number of hash functions we use to map a key to k different positions in the array
The rate of the false positives will be approximately
Let’s see why. After a single bit has been stored in the bloom filter with a capacity of m bits, the probability that a specific bit is set to 1 is 1/m. Then the probability that the same bit is set to 0 after all the k bits used to store an element have been flipped is (1–1/m)^k.
If we consider the events of flipping any specific bit to 1 as independent events, then after inserting n elements, for each individual bit the probability that the bit is still 0 is:
To have a false positive, all the k bits corresponding to an element V must have been set to 1 independently, and the probability that all of those k bits are 1 is given by:
Choosing the size of the bloom filter
To choose the size of a bloom filter, we:
Choose an estimate value for n
Choose a value for m
Calculate the optimal value of k
Calculate the error rate for the chosen values of n, m, and k. If it’s unacceptable, return to step 2 and change m; otherwise we’re done.
Thomas Hurst has a nice online page that will help you choose an optimal size for your filter, or explore how the different parameters interact.
Time and Space Complexity
Let’s say we’re using a bloom filter with m bits and k hash functions, then insertion and search will both take O(k) time. We just need to run the input through all of the hash functions and then check the output bits.
If we make a bloom filter where k=1 then we just have a hash table that ignores collisions. The lower the false positive rate low, the larger the m. So, the space of the actual data structure is simply O(m).
Possible Implementation
Let’s first define an interface for our implementation. Firstly, we’re going to need a method to add a key and one to check if the key exists. PrintStats() will print the number of total items we have added to the filter and the total number of bits sets. SetHashFunction() allows us to set a custom hash function and Reset() to clear the bloom filter.
type Bloom interface {
Add(key []byte) Bloom
Check(key []byte) (bool, float64)
PrintStats()
SetHashFunction(hash.Hash)
Reset()
}
func K(e float64) uint {
return uint(math.Ceil(math.Log2(1 / e)))
}
func M(n uint, p, e float64) uint {
// m =~ n / ((log(p)*log(1-p))/abs(log e))
return uint(math.Ceil(float64(n) / ((math.Log(p) * math.Log(1-p)) / math.Abs(math.Log(e)))))
}And now let’s dive into the implementation. We’ll define a BloomFunction with the following attributes:
h = hash function
m = number of bits in the bloom filter, will be divided into k partitions, or slices
k = number of hash values we use to set and test bits
s = the size of the partition, or slice; s = m / k
p = the fill ratio of the filter partitions. It’s mainly used to calculate m at the start. p is not checked when new items are added. So if the fill ratio goes above p, the likelihood of false positives (error rate) will increase. By default, we use the fill ratio of p = 0.5
e = the desired error rate of the bloom filter. The lower the e, the higher the k. By default, we use the error rate of e = 0.1% = 0.001.
n = number of elements the filter is predicted to hold
b = b is the set of bit array holding the bloom filters. There will be k b’s. We’re going to use the golang’s bitset package which is a mapping between non-negative integers and boolean values.
c = number of items we have added to the filter
bs = the list of bits
type BloomFunction struct {
// h is the hash function
h hash.Hash
// the total number of bits for the bloom filter.
m uint
// the number of hash values used to set and test bits.
k uint
// the size of the partition, or slice.
s uint
// the fill ratio of the filter partitions.
p float64
// the desired error rate of the bloom filter.
e float64
// number of elements the filter is predicted to hold
n uint
// b is the set of bit array holding the bloom filters.
b *bitset.BitSet
// number of items we have added to the filter
c uint
// the list of bits
bs []uint
}
var _ Bloom = (*BloomFunction)(nil)
func NewBloomFilter(n uint) Bloom {
var (
p float64 = 0.5
e float64 = 0.001
k uint = K(e)
m uint = M(n, p, e)
)
return &BloomFunction{
h: fnv.New64(),
n: n,
p: p,
e: e,
k: k,
m: m,
b: bitset.New(m),
bs: make([]uint, k),
}
}When adding an item we simply pass it through the hash functions and store the results. To check if an item is in the set we iterate through the bitset and check whether every bit is set or not. If any of the bits are not, then it’s safe to assume the word doesn’t exist. If all bits are set then the item possibly exists with the probability of the formula we proved earlier.
func (f *BloomFunction) SetHashFunction (h hash.Hash) {
f.h = h
}
func (f *BloomFunction) Reset() {
f.k = K(f.e)
f.m = M(f.n, f.p, f.e)
f.b = bitset.New(f.m)
f.bs = make([]uint, f.k)
if f.h == nil {
f.h = fnv.New64()
} else {
f.h.Reset()
}
}
func (f *BloomFunction) Add(item []byte) Bloom {
f.bits(item)
for _, v := range f.bs[:f.k] {
f.b.Set(v)
}
f.c++
return f
}
func (f *BloomFunction) Check(item []byte) (bool, float64) {
f.bits(item)
for _, v := range f.bs[:f.k] {
if !f.b.Test(v) {
return false, 0
}
}
fPosProb := math.Pow(1.0-math.Pow(1.0-1.0/float64(f.m), float64(f.k*f.n)), float64(f.k))
return true, fPosProb
}
func (f *BloomFunction) Count() uint {
return f.c
}
func (f *BloomFunction) PrintStats() {
fmt.Printf("m = %d, n = %d, k = %d, s = %d, p = %f, e = %f\n", f.m, f.n, f.k, f.s, f.p, f.e)
fmt.Println("Total items:", f.c)
c := f.b.Count()
fmt.Printf("Total bits set: %d (%.1f%%)\n", c, float32(c)/float32(f.m)*100)
}
func (f *BloomFunction) bits(item []byte) {
f.h.Reset()
f.h.Write(item)
s := f.h.Sum(nil)
a := binary.BigEndian.Uint32(s[4:8])
b := binary.BigEndian.Uint32(s[0:4])
for i := range f.bs[:f.k] {
f.bs[i] = (uint(a) + uint(b)*uint(i)) % f.m
}
}Now let’s add 2 words to the filter “hello” and “world”. We can see that the “hello” word exists with a false positive probability of 0.001.
func main() {
bf := NewBloomFilter(10)
bf.Add([]byte("hello"))
bf.Add([]byte("world"))
check, prob := bf.Check([]byte("hello"))
if check {
fmt.Printf("Word exists with a false positive probability of %v\n", prob)
} else {
fmt.Printf("Word does not exists.")
}
}
bf.PrintStats()
// Prints
/*
Word exists with a false positive probability of 0.0010134325478480376
m = 144, n = 10, k = 10, s = 0, p = 0.500000, e = 0.001000
Total items: 2
Total bits set: 20 (13.9%)
*/Code available on github.
Applications
In BigTable (and Cassandra), any read operation has to read from all SSTables that make up a Tablet. If these SSTables are not in memory, the read operation may end up doing many disk accesses. To reduce the number of disk accesses, BigTable uses Bloom filters. (source)
Bloom filters are created for SSTables (particularly for the locality groups). They help reduce the number of disk accesses by predicting if an SSTable may contain data corresponding to a particular row or column pair. For certain applications, a small amount of Tablet server memory used for storing Bloom filters drastically reduces the number of disk-seeks, thereby improving read performance.
Medium uses Bloom filters in its Recommendation module to avoid showing the posts that the user has already seen.